Définition
L’optimisation est une branche des mathématiques, dont me but est de trouver analytiquement une numériquement la meilleure solution (l’optimale) à un problème donné.
L’origine du mot optimal provient du latin optimum qui signifie le meilleur
Un problème d’optimisation consiste, étant donné une fonction , à trouver :
- Son minimum (resp. son maximum) dans
- Un point qui réalise ce minimum (resp. maximum) i.e
Vocabulaire :
- est la fonction objectif
- solution réalisables du problème
- est la solution optimale
La recherche opérationnelle (RO)
La Recherche Opérationnelle est la discipline des méthodes scientifiques utilisables pour faciliter la prise de décisions face à des problématiques qui se rencontrent dans les grandes organisations publiques ou privées.
Discipline transverse associant les mathématiques appliquées, les statistiques et l’informatique, elle s’applique à des problèmes usuels et joue un rôle clé dans la recherche de l’efficience.
La Recherche Opérationnelle permet notamment d’optimiser l’architecture et le fonctionnement des organisations.
Grâce à elle, les décideurs peuvent analyser et mieux comprendre des situations complexes ou de grandes dimensions, aux interactions nombreuses et donc, de faire des choix pertinents en toute connaissance de cause.
Elle participe à l’aide de décision
La RO-AD (Recherche Opérationnelle - Aide à la Décision) est omniprésente dans des secteurs de plus en plus variés comme :
- L’informatique, l’industrie
- Le transport, la santé, les télécommunications, la distribution, la banque, la finance, l’assurance.
Etapes d’une étude de RO
- Modélisation du problème
à partir d’un problème concret, bâtir un modèle scientifique (en général mathématique, mais aussi graphique…) représentant schématiquement la réalité ;
- Résolution du problème : Résoudre le modèle ainsi construit
résolution = mise en œuvre de méthodes numériques permettant d’obtenir des réponses effectives
Les grandes classes de problèmes d’optimisation
- Les problèmes de sac à dos
- Les problèmes de tournés
- Les problèmes d’affectation
- Les problèmes d’ordonnancement
- Les problèmes de file d’attente
- Les problèmes de flot
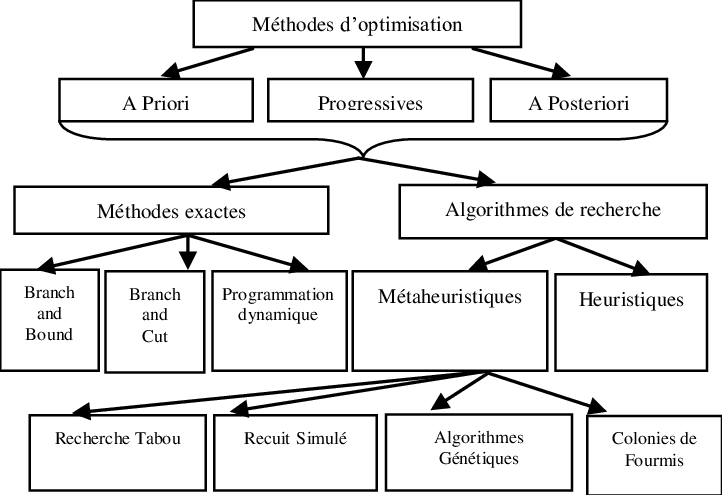
Méthodes d’optimisations possibles
Deux grandes familles de méthodes :
- Méthodes exactes (basées sur des principes mathématiques)
- Méthodes approchées ou heuristiques (sont souvent stochastiques (=hasard); quand les méthodes exactes ne sont pas disponibles, ou sont trop coûteuses ; souvent le cas)